1.2 Getting Started

Imagine the old-school way of writing a mathematical formula or expression on a chalkboard. Under it, another expression is written, derived mathematically from the first one. Then, in a succession of refining steps, more expressions are written until a final result is achieved. Sometimes chalk marks, strikeouts and other notations show how each expression relates to the next. The collection of expressions illustrates a path of mathematical thinking. From the implied relationship between each expression, the reader infers the application of some mathematically correct transformation.

It is this way of doing mathematics that is captured in Myron. The blackboard analogy translates to Myron through the activity of selection and the application of transformations.

Selection has interactive, visual and mathematical aspects.

• Interactively, a selection is made by touching part of an expression. A selection is extended by touching another part of the expression that is related mathematically to the existing selection or by touching the selection a second time. A selection is changed to a completely different selection by touching another part of the expression that is not related to the existing selection or by touching a different expression.
• Visually, a selection is displayed using some form of highlighting. This indicates the selection of a single operand (like this: x+.{y}+z), of an operator and its operands (like this: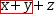 .{x+y}+z) or of multiple operators and all their operands (like this: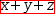 .{x+y+z}). Highlighting can take the form of underlining, boxing, colour change or other display-dependent facility.
• Mathematically, a selection is a subexpression of some larger expression, or the entire expression itself.

Once a selection has been made, a transformation is applied by activating a user-interface control like a button or a menu item.

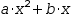
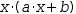
A transformation is a change to the form of an expression that preserves the mathematical meaning of the expression. For example, the expression a⋅x^2+b⋅x has the same meaning as x⋅(a⋅x+b) under the rules of algebra. Transforming an expression like the first one into the second one is called factoring (see §3.2.4). The inverse of this, transforming an expression like the second one into the first one, is called distribution (see §3.2.3).

The remainder of this chapter provides a quick tour through Myron's user interface. The next chapter introduces Myron's expression language and its major expression constructs. The third chapter begins with a description of the most important and frequently used transformations; the rest of the third chapter covers the transformations provided from menu items. Subsequent chapters describe more transformations and techniques for working with Myron. Finally, Myron's capability with respect to the file system and the cloud is described.